Part E: 反演作圖(Inverse Points)

※反演點的定義：在空間(Normed Space)中，給定點O、常數R，

　點P的反演點Q就是在直線OP上使得||OP||‧||OQ|| = R²的點。

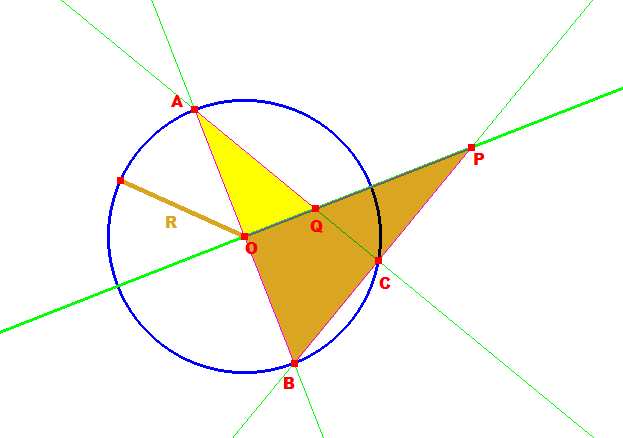　在平面上的展示：(點擊圖片可以看解說)

反演點作圖

　　※給定點O和常數R可以試為給定圓O(或球)。

　　※這裡為了方便以下展示，所以採用此反演作圖法。

　　　一般採用此種方式解說：http://mathworld.wolfram.com/InversePoints.html

(a)將平面上某些點的集合作其反演(給定點O和常數R)：

圓的反演是圓(或直線)	直線的反演是過O點的圓

(b)推廣到空間上(一樣給定點O和常數R)：

球的反演是球(或平面)	平面的反演是過O點的球	圓的反演是圓(或直線)	直線的反演是過O點的圓

　　※問題：在三度空間中，給定點O和常數R，若圓A的反演為圓B，則這兩個圓是否位於同一球面？

(c)問題討論：

(1)球面上的圓對空間中另一點 在球面上的投影	(2)定裡發現	(3)問題解答

※問題：在其他空間中是否也可以定義反演點？這些性質是否也成立？ In Metric Space?  In Vector Space?

(d)Poler Plane