| Geometric Construction | |
| Teacher | 全任重 老師 |
| Student | 康耀文 |
| ID | 9861234 |
Week 1
| Dual For Cube |
Rhombic triacontahedron |
Cube & tetrahedron |
rhombic icosahedron in regular octahedron in regular tetrahedron in cube in rhombic dodecahedron |
Cube distortion |
Animation of Rhombic Polyhedron with 132 Rhombic faces |
 |
 |
 |
 |
 |
 |
Week 2
No Class
Week 3
Week 4
| Samll Rhombicosidodecahedron |
Great Rhombicosidodecahedron |
Dodecahedron by Icosahedron |
Tetrahedron 5-Compound |
Faces of Icosahedron lie on Faces of Five Tetrahedra |
Octahedron 5-Compound |
 |
 |
 |
 |
 |
 |
| Octahedron 5-Compound (Method 2) | 5 Cube inside Regular Dodecahedron |
5 Cube inside Regular Dodecahedron (Method 2) | |||
 |
 |
 |
Week 5
| Greatest Cube Inside an Regular Dodecahedron (Method 1) |
Greatest Cube Inside an Regular Dodecahedron (Method 2) |
Greatest Regular Dodecahedron Inside an Cube (Method 1) |
Greatest Regular Dodecahedron Inside an Cube (Method 2) |
Greatest Octahedron Inside an Cube (Method 1) |
Greatest Octahedron Inside an Cube (Method 2) |
 |
 |
 |
 |
 |
 |
| Greatest Icosahedron Inside an Tetrahedra (Method 1) | Greatest Icosahedron Inside an Tetrahedra (Method 2) | Greatest Icosahedron Inside an Octahedron |
Cube Projected on Cube(Method1) | Cube Projected on Cube(Method2) | Cube Projected on Regular Dodecahedron |
 |
 |
 |
 |
 |
 |
Week 6
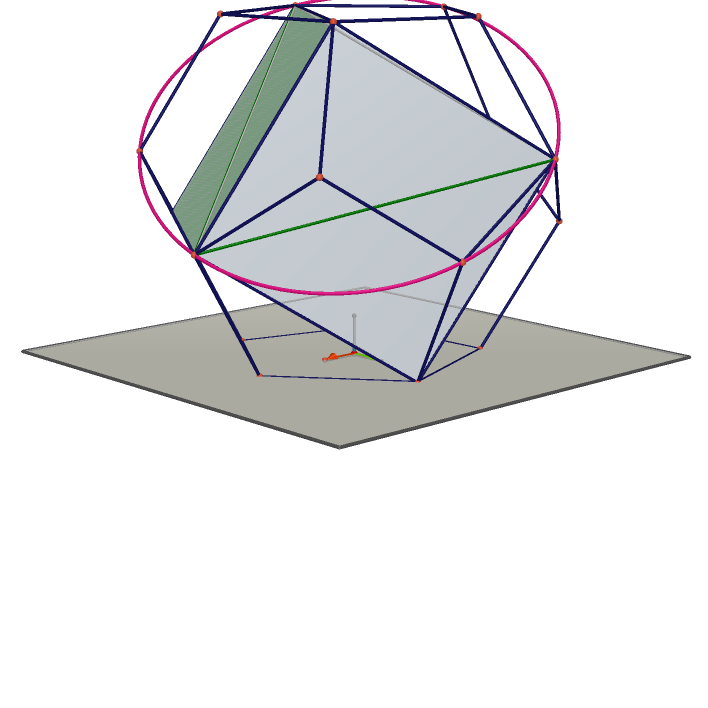
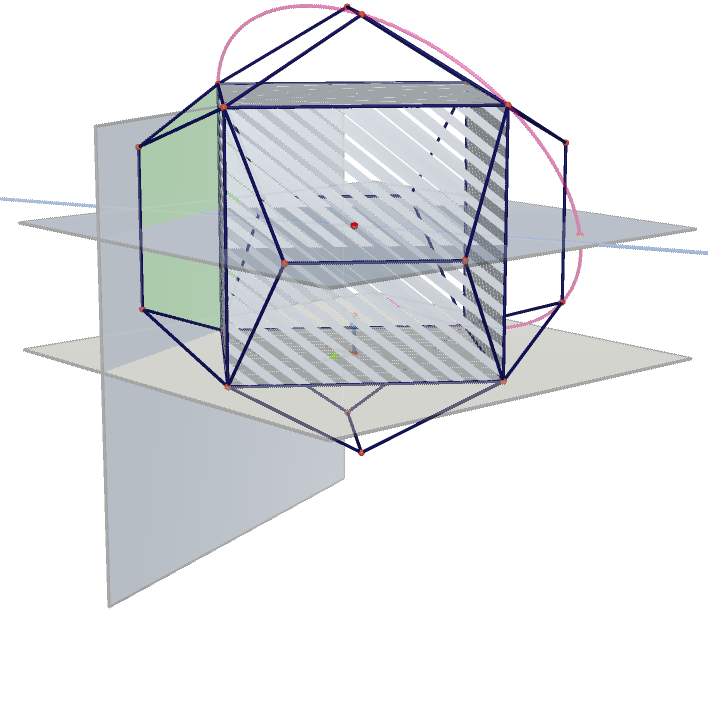
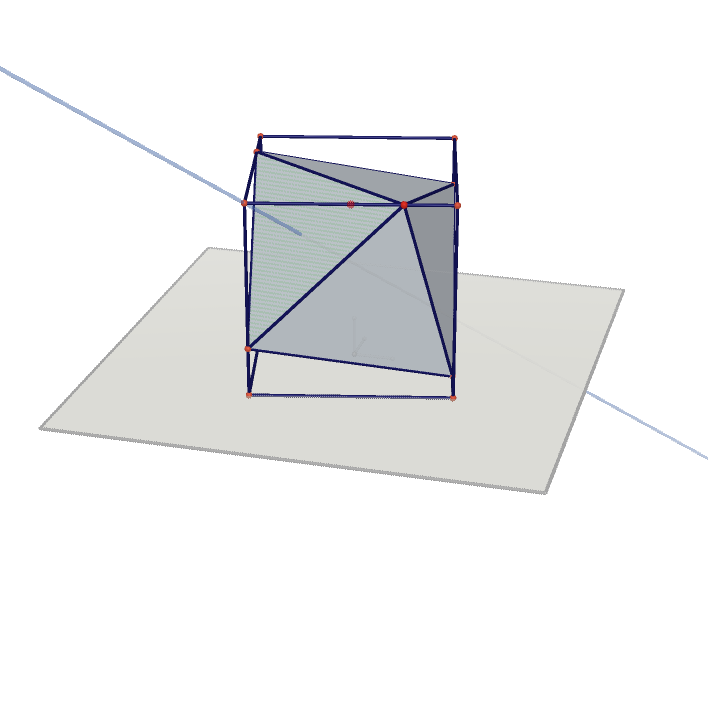
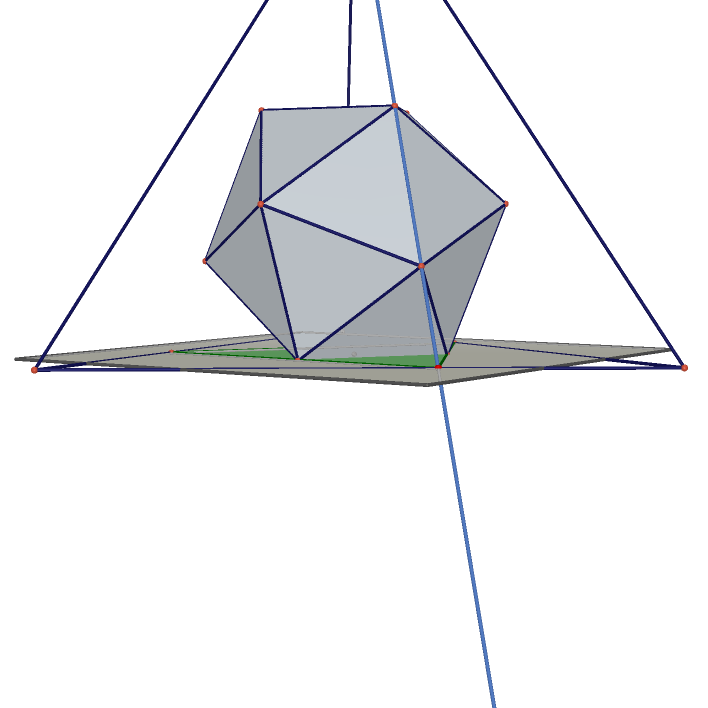
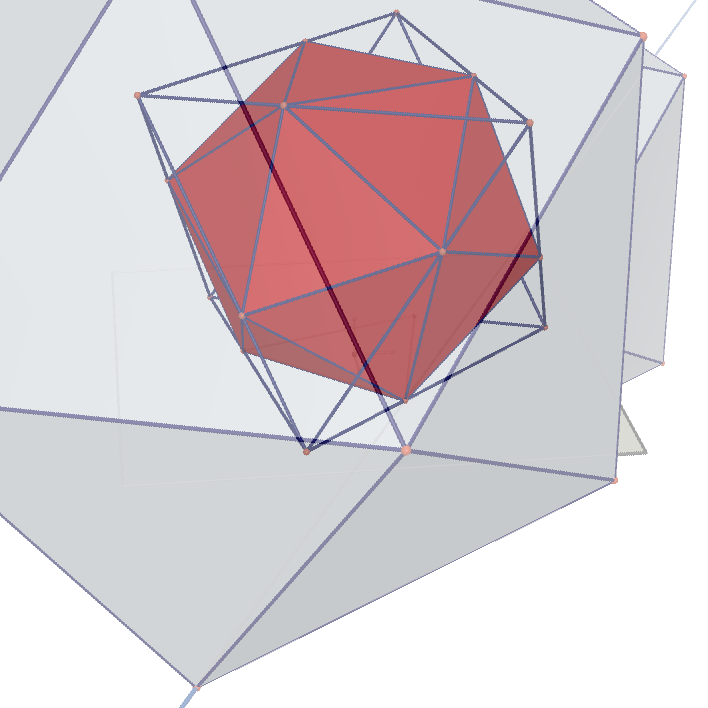
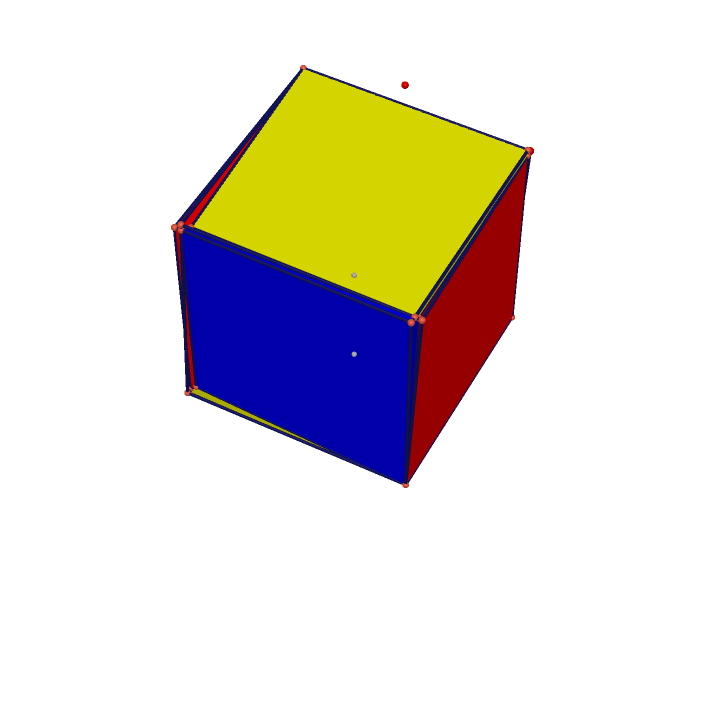
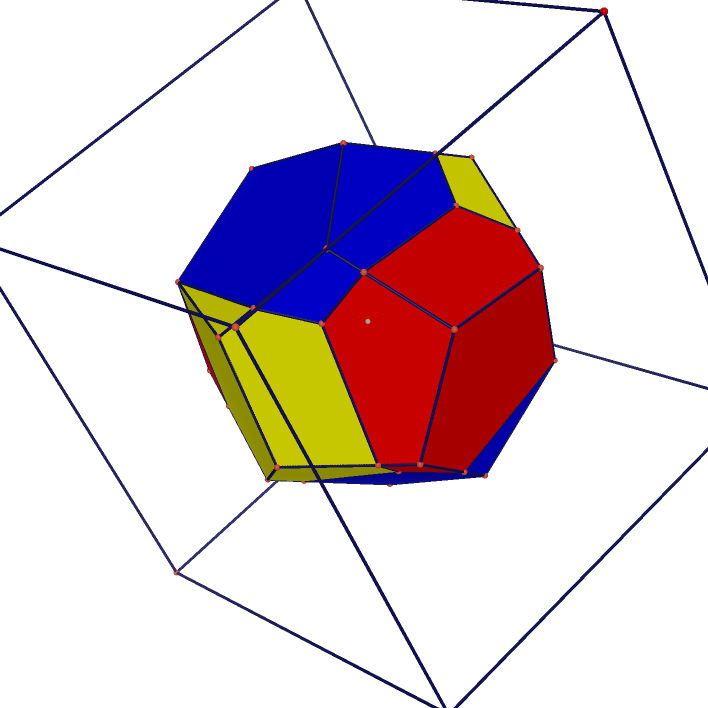
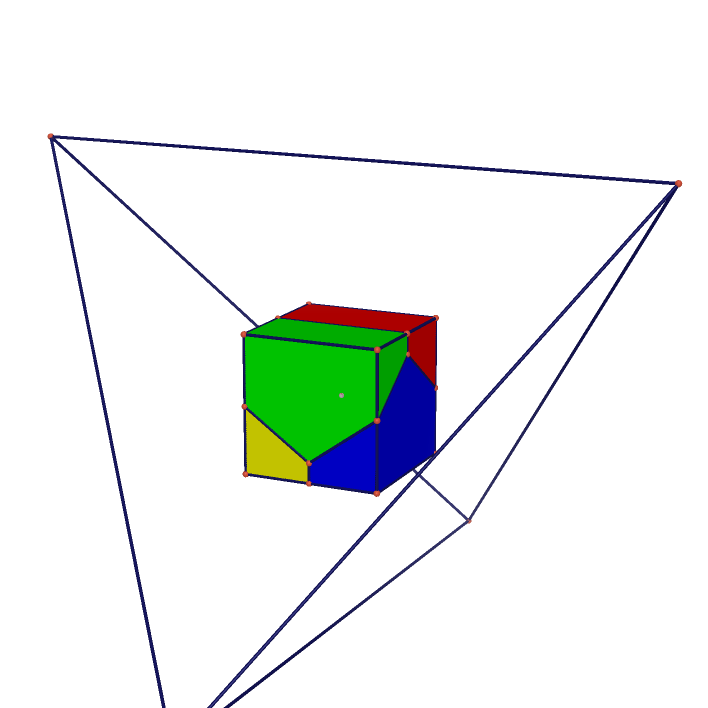
| Tetrahedron Projected on Tetrahedron | Tetrahedron Projected on Cube | Cube Projected on Rhombic Dodecahedron |
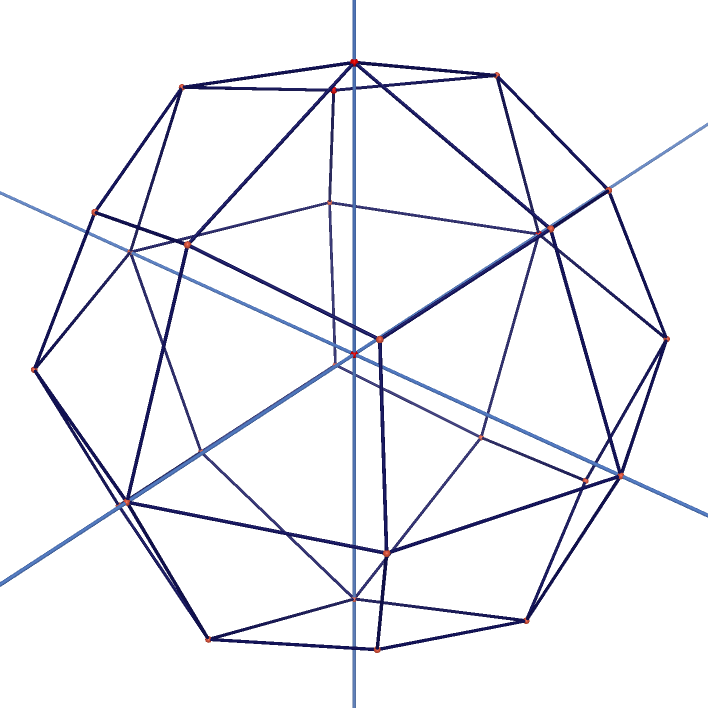
Cube Projected on Rhombic triacontahedron | Icositetrahedron | Animation of Icositetrahedrons |
 |
 |
 |
 |
 |
 |
Week 7
| Inspired by Paper Folding |
Adjustable Kaleidocycles-5 | Adjustable Tight Kaleidocyle |
Jitterbug |
 |
 |
 |
 |
Week 8
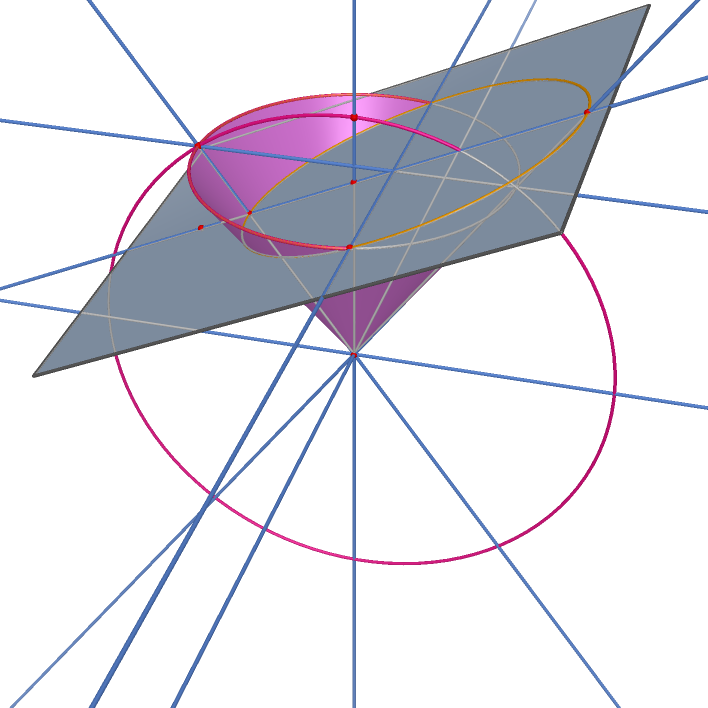
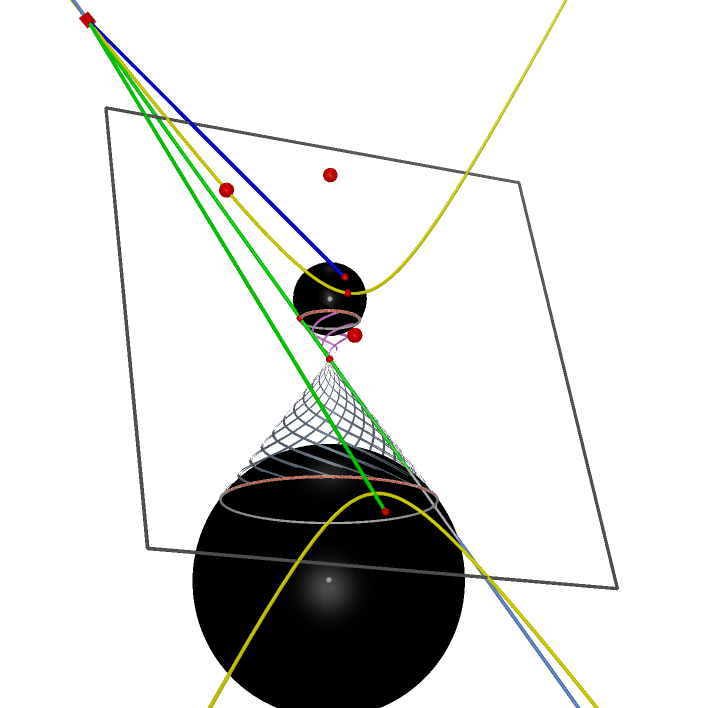
| A Parabola in 3-Dimensional Space |
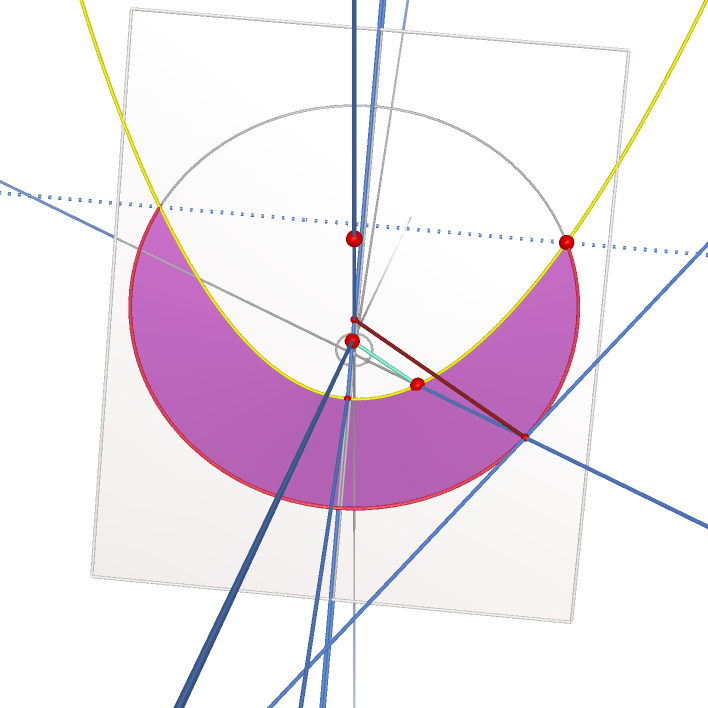
Conic Section |
A Parabola trajectory in 3-Dimensional Space |
 |
 |
 |
Week 9
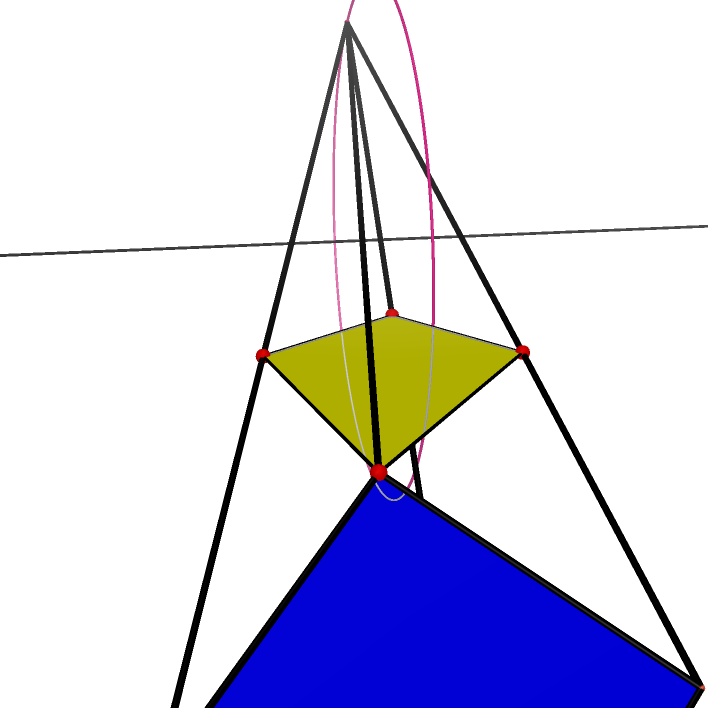
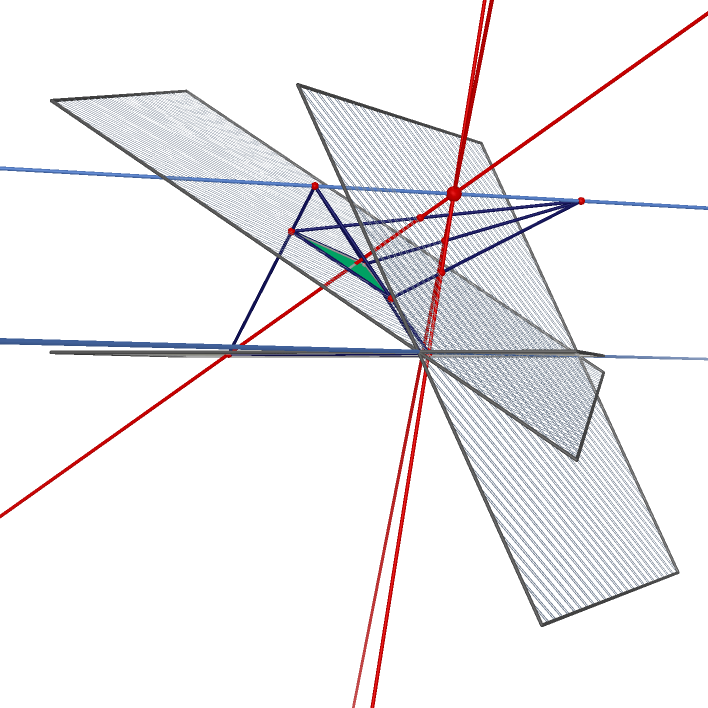
| Two Perspetive Quadrilaterals Having One Point in Common |
Desargues' Theorem in 3D |
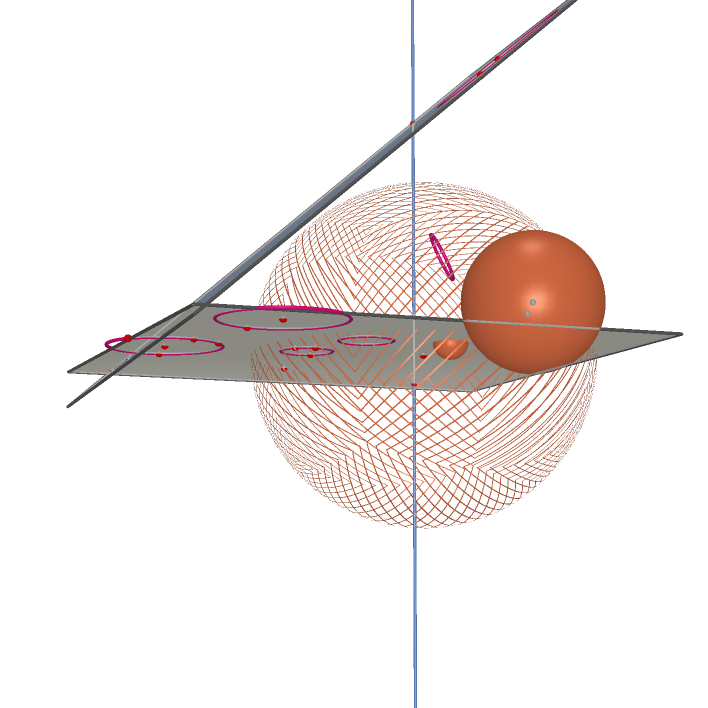
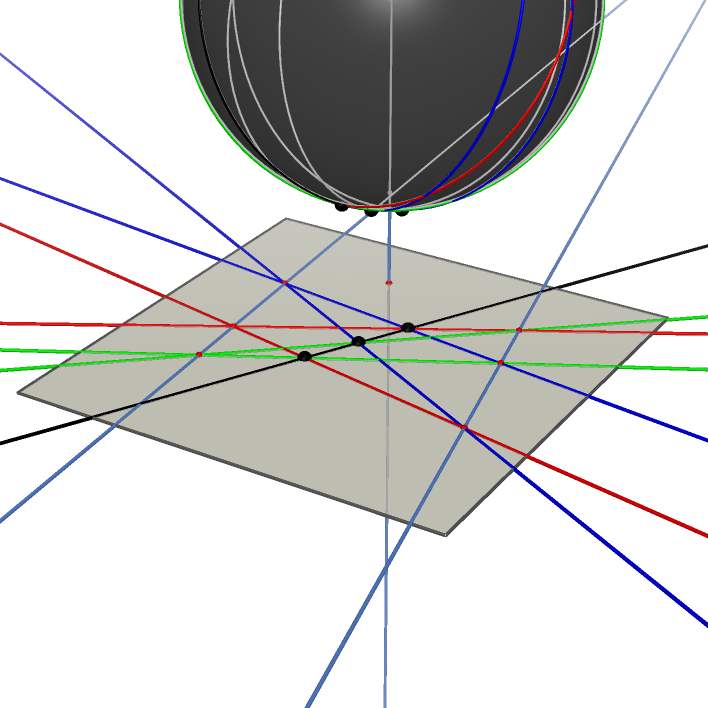
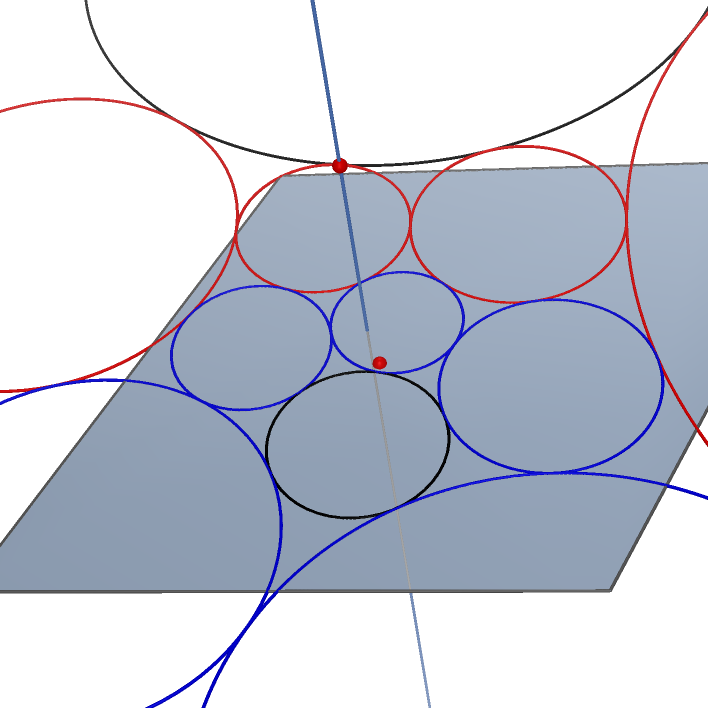
Common Tangent Cones of Three Spheres |
 |
 |
 |
Week 10
| Circle projection to a point on the sphere |
Inversion practice I |
Inversion practice II | Inversion circle will be the projection to the center of orthogonal sphere |
Three-Circle Theorem on Sphere |
Three-Circle Theorem on Sphere II |
 |
 |
 |
 |
 |
 |
Week 11
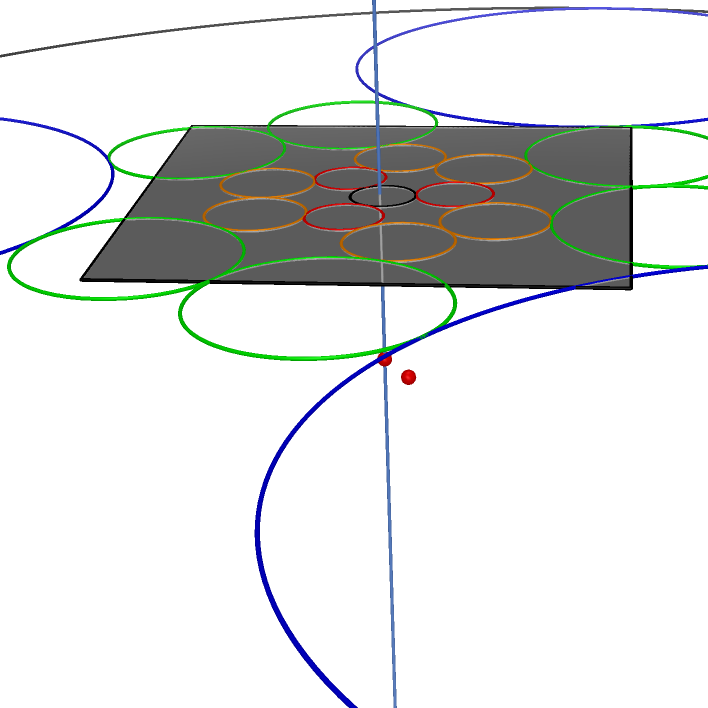
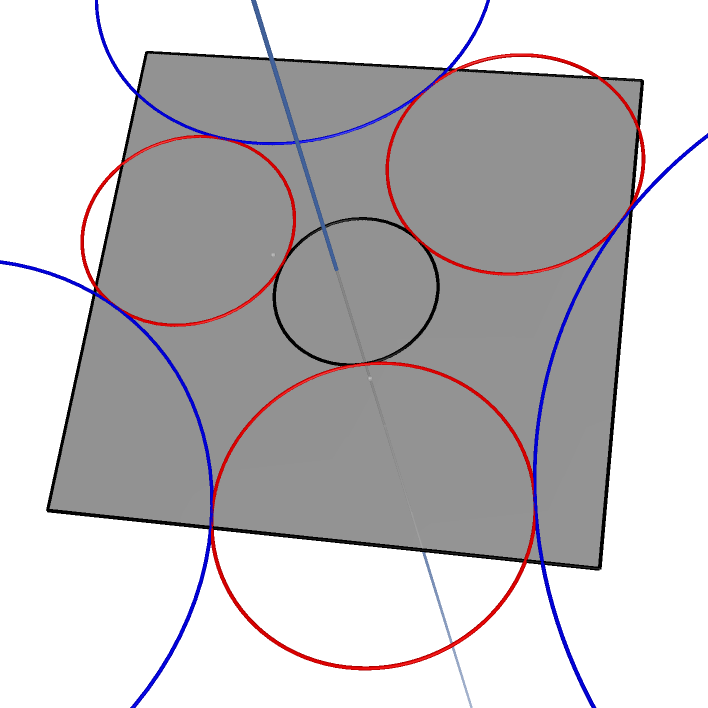
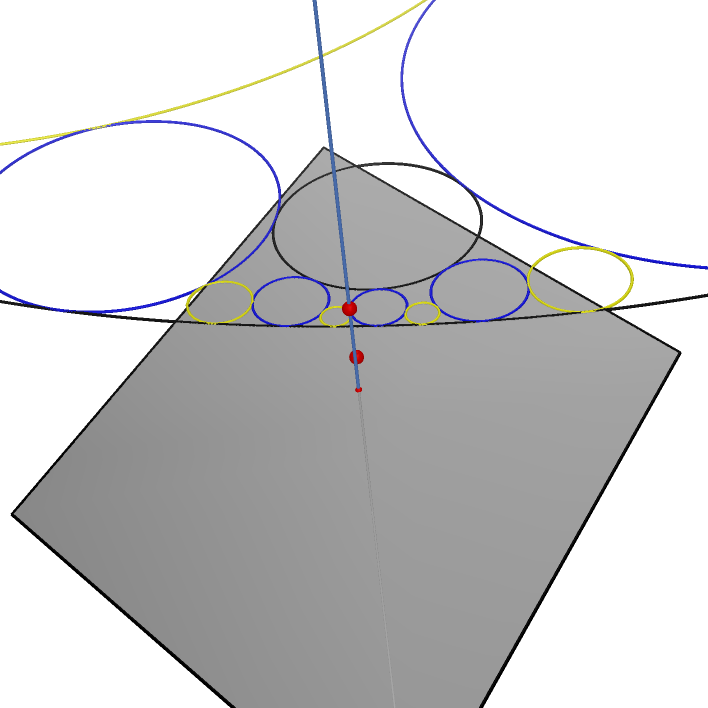
| Steiner Porism I |
Steiner Porism II | Three Triangulars of two circles and their inverse relative to the sphere |
 |
 |
 |
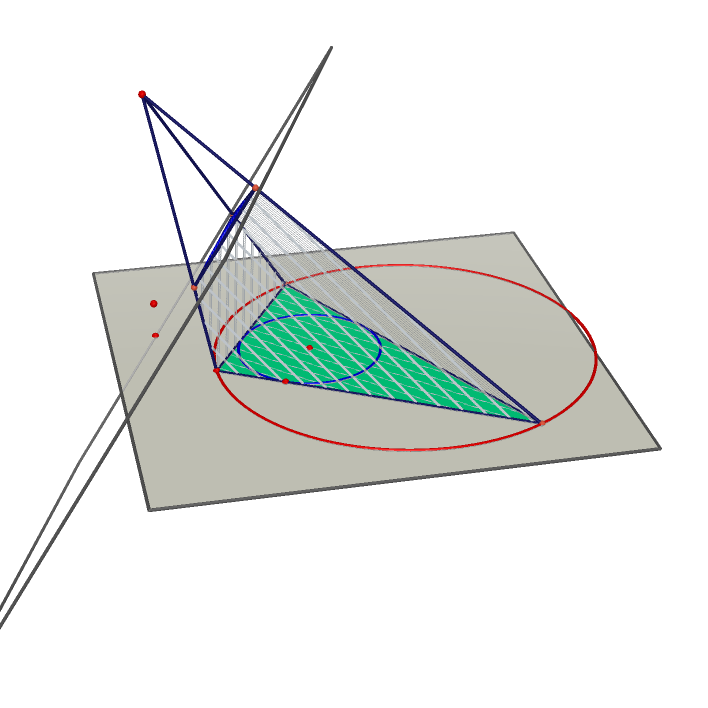Week 12
| Circle Trajectory in lateral direction |
Circle Trajectory in vertical direction | Villarceau circles |
Villarceau circles-12 |
Triangle Torus and Tangent |
|
 |
 |
 |
 |
 |
 |
| Trajectory of intersection curve of sphere and the plane which is perpendicular to diameter | Trajectory of intersection curve of sphere and the plane outside the sphere | Trajectory of intersection curve of sphere and the plane which orthogonal to the sphere with a line | |||
 |
 |
 |
Week 13
| Inversion
wrt big sphere of a circle is the projection on the small sphere,which
means small sphere is the inversion of plane |
The
relation of the circles on the plane is same as the relation of
inversion circles on small sphere which is the inversion of the plane |
Four Circles Each Common Tangent to Two Fixed Circles and Their Stereographic Images |
Circles and there Inversion Relationship |
Inversion of Circles of 6 different connect points in two intersecting line |
 |
 |
 |
 |
 |
Week 14
| Asymmetric Steiner Porism |
Inversion of Circles Inscribed in the Faces of Regular Icosahedron | Inversion of Circles Inscribed in the Faces of Regular Octahedron |
Inversion of Inscribed Circles of Faces of Square Cupola |
Inversion of Inscribed Circles of Faces of Great Rhombicuboctahedron |
 |
 |
 |
 |
 |
Week 15
Sick Leave
Week 16
| Two circles on sphere inversed by the orthogonal sphere with same axis |
Asymmetric Design Based on Regular Octahedron | Asymmetric Design Based on Triangular Cupola |
 |
 |
 |
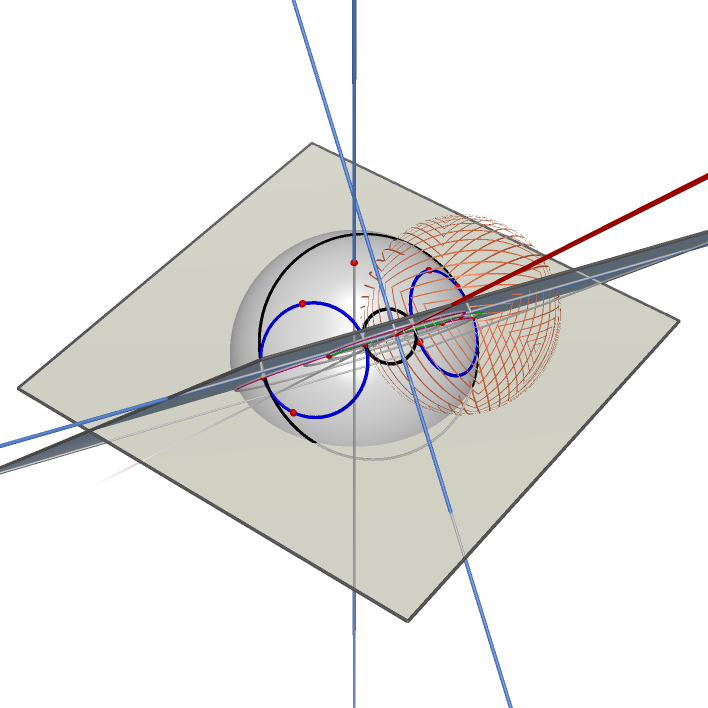
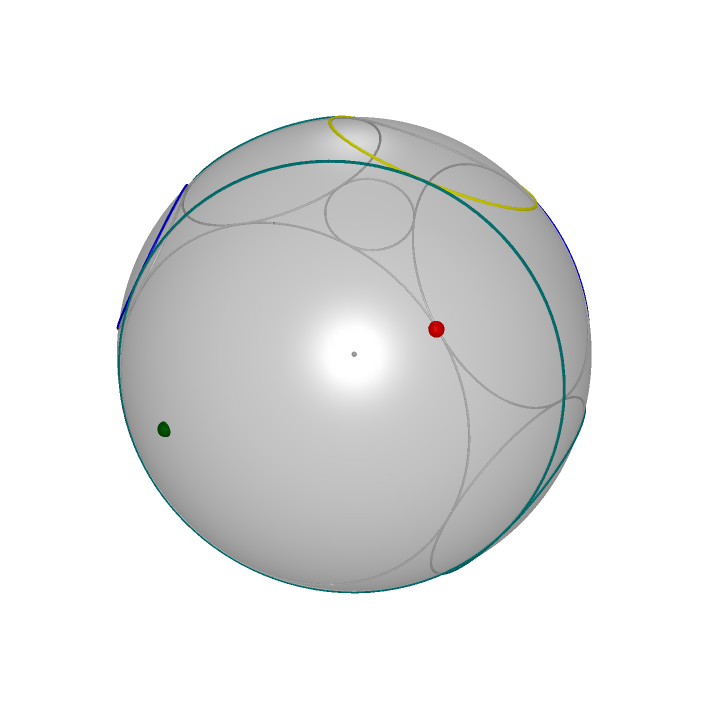